How to Complete Ridge Regression Assignments Using SAS

Understanding Ridge Regression

Ridge regression is an essential method for handling multicollinearity in regression analysis. Unlike ordinary least squares, which can produce inflated and erratic coefficient estimates when predictors are correlated, ridge regression stabilizes these estimates by introducing a penalty term. This section explains the fundamentals of ridge regression, including its mathematical formulation and key advantages. Understanding these concepts is critical before moving on to practical implementation in SAS.

What Is Ridge Regression?

Ridge regression, also known as L2 regularization, modifies the OLS loss function by adding a penalty term proportional to the square of the coefficients. The penalty term (λ) controls the amount of shrinkage applied to the coefficients, reducing their variance at the cost of introducing some bias.

The ridge regression equation is:

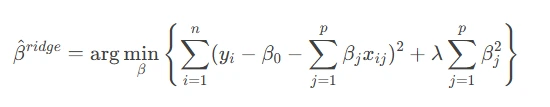
Why Use Ridge Regression?

Ridge regression is particularly useful when:

• Predictors are highly correlated (multicollinearity).
• The dataset has more predictors than observations (high-dimensional data).
• OLS estimates have high variance, leading to overfitting.

By shrinking coefficients, ridge regression improves model generalizability while maintaining predictive accuracy.

Implementing Ridge Regression in SAS

Once the theoretical foundation of ridge regression is clear, the next step is applying it using SAS. This section provides a step-by-step guide on preparing data, writing SAS code, and executing ridge regression analysis. Proper data preprocessing and understanding SAS syntax are crucial for obtaining reliable results. Following these steps ensures that students can confidently replicate the process in their assignments.

Preparing the Data for Analysis

Before applying ridge regression, ensure the dataset is properly formatted:

• Standardize continuous predictors (mean = 0, standard deviation = 1) to ensure fair penalization.
• Handle missing values appropriately (e.g., deletion or imputation).
• Split data into training and validation sets if cross-validation is needed.

Using PROC REG for Ridge Regression

SAS provides the PROC REG procedure with the RIDGE= option to perform ridge regression. Below is a sample code:

/* Standardize variables and apply ridge regression */ PROC STDIZE DATA=mydata OUT=std_data METHOD=STD; VAR x1 x2 x3; RUN; PROC REG DATA=std_data OUTEST=ridge_results; MODEL y = x1 x2 x3 / RIDGE=0.1 TO 1 BY 0.1; RUN;

RIDGE= specifies the range of lambda values.

The OUTEST= option stores coefficient estimates for different λ values.

Interpreting Ridge Regression Results

After running ridge regression in SAS, the next challenge is interpreting the output correctly. This section explains how to analyze coefficient shrinkage, select the optimal lambda value, and assess model performance. Proper interpretation ensures that students can draw meaningful conclusions from their analysis and justify their choices in assignments.

Analyzing Coefficient Shrinkage

As λ increases, coefficients shrink toward zero. A ridge trace plot helps visualize how coefficients change with different λ values. The optimal λ balances bias and variance, often selected using cross-validation.

To generate a ridge trace plot in SAS:

PROC PLOT DATA=ridge_results; PLOT x1*_RIDGE_ x2*_RIDGE_ x3*_RIDGE_ / OVERLAY; RUN;

Selecting the Best Lambda Value

The optimal λ minimizes prediction error. SAS does not automatically perform cross-validation for ridge regression, but you can use:

• Generalized Cross-Validation (GCV) – Available in some SAS procedures.
• Manual k-fold cross-validation – Split data into training/test sets and evaluate mean squared error (MSE) for different λ values.

Comparing Ridge Regression with Other Methods

Understanding how ridge regression compares to other regularization techniques helps in selecting the right method for a given problem. This section contrasts ridge regression with OLS and Lasso regression, highlighting their respective strengths and weaknesses. Such comparisons are often required in assignments to demonstrate a comprehensive understanding of regression techniques.

Ridge vs. OLS Regression

• OLS provides unbiased estimates but suffers from high variance with multicollinearity.
• Ridge introduces bias but reduces variance, improving model stability.

Ridge vs. Lasso Regression

• Ridge shrinks coefficients but rarely sets them to zero.
• Lasso (L1 regularization) can perform variable selection by shrinking some coefficients to exactly zero.

For datasets with many irrelevant predictors, Lasso may be preferable, while Ridge works better when all predictors are relevant but correlated.

Conclusion

Ridge regression serves as an indispensable technique for addressing multicollinearity challenges in regression analysis. By introducing a carefully controlled bias through its penalty parameter (λ), this method produces more stable coefficient estimates while maintaining strong predictive performance. The SAS software provides robust capabilities for implementing ridge regression through its PROC REG procedure, complete with features for generating ridge trace plots and evaluating different λ values. When working to solve your Statistics assignment, pay particular attention to three critical aspects: first, ensure all predictors are properly standardized to allow for meaningful coefficient comparisons; second, methodically determine the optimal λ value through cross-validation techniques; and third, understand how ridge regression compares to both OLS and Lasso approaches in terms of variable selection and coefficient shrinkage.

Mastering these elements not only helps complete current assignments but also builds a strong foundation for tackling more advanced statistical modeling tasks. The combination of theoretical understanding and practical SAS implementation skills demonstrated in this guide will enable you to confidently approach ridge regression problems and deliver accurate, well-justified solutions in your academic work. Remember that proper application of these techniques can make the difference between adequate and outstanding results in your statistical analyses.