How to Improve Regression Assignment Accuracy Through Variable Standardization

Why Standardizing Variables Matters in Regression

When working with regression models, predictors often come in different units. For example, in a study predicting house prices, you might have variables like:

• Square footage (measured in hundreds or thousands)
• Number of bedrooms (typically 1-5)
• Distance from the city center (in miles or kilometers)

If you fit a regression model with these raw values, the coefficients will reflect the original scales. A coefficient of 10,000 for square footage might seem huge compared to a coefficient of -5,000 for distance, but this doesn’t necessarily mean square footage is more important—it’s just measured differently.

Standardizing variables puts them all on the same scale (usually mean = 0, standard deviation = 1), allowing for fairer comparisons.

How Standardization Affects Coefficient Interpretation

After standardization:

• Each coefficient represents the expected change in the dependent variable for a one-standard-deviation increase in the predictor.
• The intercept becomes the predicted value when all predictors are at their mean.

For example, if the standardized coefficient for education level is 0.4 and for income is 0.6, we can say income has a stronger effect because a one-SD increase in income leads to a larger change in the outcome than a one-SD increase in education.

When Standardization Is Necessary

Standardization is particularly useful in these scenarios:

• Comparing predictor importance – When you need to assess which variables have the strongest influence.
• Regularized regression (Ridge/Lasso) – These methods penalize coefficients based on their magnitude, so scaling ensures fair shrinkage.
• Interaction terms & polynomial regression – Helps avoid multicollinearity from higher-order terms.
• Algorithms using gradient descent – Standardization helps optimization converge faster.

However, it’s not always required for simple linear regression if your only goal is prediction (not interpretation).

How to Standardize Variables in Regression

The most common standardization method is the z-score transformation:

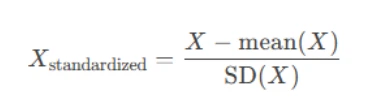
This centers the variable at 0 and scales it so that one unit equals one standard deviation.

Step-by-Step Standardization Process

• Calculate descriptive statistics – Compute the mean and standard deviation for each predictor.
• Center the variables – Subtract the mean from each observation.
• Scale by standard deviation – Divide the centered values by the SD.

Example:

Suppose we have a variable "Test Scores" with mean = 75 and SD = 10.

A raw score of 85 becomes: (85−75)/10=1

A score of 65 becomes: (65−75)/10=−1

Now, all values are in standard deviation units.

Implementing Standardization in Statistical Software

Most statistical packages have built-in functions for standardization:

In R:

data$var_standardized <- scale(data$var)

In Python (scikit-learn):

from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_standardized = scaler.fit_transform(X)

In SPSS:

Use Analyze → Descriptive Statistics → Descriptives

Check "Save standardized values as variables"

Important Note: Always standardize after splitting data into training and test sets to avoid data leakage.

Advantages of Standardized Regression Coefficients

Standardized regression offers several key benefits for assignments and real-world analysis.

• Easier Comparison of Predictor Importance
• When variables are on the same scale:
• Coefficients directly show which predictors have the strongest effect.
• You can rank variables by their absolute coefficient values.

Example:

In a model predicting job satisfaction, suppose we get these standardized coefficients:

• Salary: 0.45
• Work-Life Balance: 0.60
• Commute Time: -0.30

This suggests work-life balance matters most, followed by salary, while longer commutes reduce satisfaction.

Improved Model Stability

Standardization helps with:

• Multicollinearity – Reduces correlation between interaction/polynomial terms.
• Gradient descent optimization – Prevents one variable from dominating updates.
• Regularization methods – Ensures Ridge/Lasso penalties apply fairly.

Conclusion

Standardizing variables is a fundamental yet powerful technique in regression analysis that can significantly enhance the quality of your statistical work, particularly when you need to do your statistics assignment with precision and clarity. By transforming predictors to a common scale, students gain several key advantages: First, it allows for fair comparison of variable importance, making it easier to identify which factors have the strongest influence on your outcome. Second, standardization helps avoid scaling-related biases, especially when working with advanced methods like regularized regression (Ridge or Lasso), where variables with larger scales might otherwise dominate the model. Third, it improves numerical stability in iterative algorithms, ensuring more reliable convergence in optimization processes.

While standardization isn't always mandatory—simple linear regression for prediction-only purposes may not require it—understanding its proper application demonstrates statistical sophistication. When used appropriately, this technique leads to more interpretable results, clearer insights, and ultimately, stronger academic performance. Whether you're working on a basic homework problem or a complex research project, mastering variable standardization will help you do your statistics assignment more effectively, producing work that stands out for its rigor and analytical depth. Remember to always consider your research question and model requirements when deciding whether standardization is necessary for your specific analysis.