How to Interpret Standardized and Unstandardized Coefficients on Statistics Assignments

Unstandardized Coefficients Explained

Unstandardized coefficients, often denoted as B or β, represent the raw change in the dependent variable for each unit increase in the independent variable, holding other variables constant. They are directly derived from the units of measurement used in the dataset.

For example, if you are examining the relationship between study hours (in hours) and exam scores (in percentage), an unstandardized coefficient of 2.5 means that for each additional hour of study, exam scores are expected to increase by 2.5 percentage points, assuming other variables remain unchanged.

Unstandardized coefficients are useful because they provide clear, real-world interpretations. They are particularly helpful when the researcher or student wants to maintain the context of the data's original scale and directly relate it to the research question at hand.

Standardized Coefficients Defined

Standardized coefficients, also called beta coefficients (β), transform the variables into a standard scale with a mean of zero and a standard deviation of one. This standardization process removes the units of measurement, allowing for direct comparisons of the relative importance of predictors in the model.

For instance, if a regression model has standardized coefficients of 0.6 for study hours and 0.3 for sleep duration, it indicates that study hours have a stronger relative impact on exam scores than sleep duration. Unlike unstandardized coefficients, these coefficients are unitless, providing a common basis for evaluating predictors in different scales.

Standardized coefficients are particularly valuable when variables are measured in different units, making direct comparisons challenging. They provide a holistic view of the predictor variables’ contributions in relative terms.

How to Calculate Standardized and Unstandardized Coefficients

Calculating standardized and unstandardized coefficients is an important skill for statistics students. These calculations provide the numerical foundation for regression analysis and influence how results are interpreted in assignments. Unstandardized coefficients are typically computed directly from regression analysis, maintaining the variables’ original units and scales. In contrast, standardized coefficients involve an extra step of standardizing the variables before or after the regression. Knowing how to compute these coefficients accurately ensures reliable conclusions and supports effective decision-making based on the data. Let’s break down the calculation methods for each type of coefficient to understand the process in depth.

Calculation of Unstandardized Coefficients

Unstandardized coefficients are obtained directly through regression analysis using the least squares method. In simple linear regression, the unstandardized coefficient is computed as:

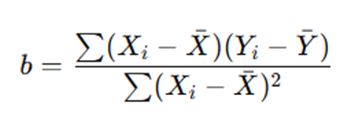
This formula reflects the slope of the regression line, representing the average change in the dependent variable for a one-unit change in the independent variable.

In multiple linear regression, the unstandardized coefficient is computed similarly but also accounts for other predictors in the model. Statistical software like R, SPSS, or Python’s statsmodels library automatically calculates these values when you run a regression analysis.

Standardizing the Coefficients

To obtain standardized coefficients, each variable (including the dependent and independent variables) is transformed into z-scores:

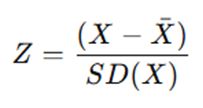
After standardizing the variables, the regression analysis is performed again, yielding standardized coefficients. Alternatively, a quicker method involves adjusting the unstandardized coefficients using the standard deviations of the variables:

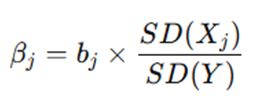
This adjustment ensures that all predictors are on the same scale, allowing for direct comparisons.

How to Interpret Standardized and Unstandardized Coefficients in Assignments

Interpreting standardized and unstandardized coefficients correctly is crucial in statistics assignments. Each type of coefficient has a specific role in understanding the relationships between variables. Unstandardized coefficients reveal real-world impacts in the data’s original units, making them useful for prediction and decision-making. Standardized coefficients, on the other hand, highlight which predictors have the strongest relative effects, regardless of units. In assignments, students need to recognize when to prioritize real-world interpretation versus comparative analysis. Let’s explore how to approach interpreting these coefficients effectively to maximize insights and accuracy in your statistics assignments.

Contextual Interpretation of Unstandardized Coefficients

In assignments involving regression analysis, interpreting unstandardized coefficients requires paying close attention to the original units of the data. For example, if the dataset involves income (in dollars) and education level (in years), an unstandardized coefficient of 1500 for education suggests that each additional year of education is associated with an average increase of $1,500 in income.

Students should note that while these coefficients provide straightforward real-world meaning, they may not be directly comparable across predictors if the predictors use different units of measurement. Therefore, careful consideration of the variable scales is essential.

Using Standardized Coefficients to Compare Predictors

Standardized coefficients are particularly helpful when students need to identify which predictors have a greater impact on the dependent variable. In assignments comparing the relative influence of variables like study hours, sleep duration, and caffeine intake on exam performance, standardized coefficients highlight the strongest predictors.

For example, if standardized coefficients are:

• Study hours: 0.5
• Sleep duration: 0.2
• Caffeine intake: 0.1

It indicates that study hours have the greatest relative influence on exam performance. In assignments requiring prioritization of predictors, standardized coefficients offer a clear path for identifying which factors warrant the most attention.

Advantages and Limitations of Standardized and Unstandardized Coefficients

Both standardized and unstandardized coefficients have unique strengths and weaknesses, making it important for students to understand their implications. Unstandardized coefficients excel at delivering precise, real-world insights that are critical for practical decision-making and forecasting. However, they cannot be compared across predictors with different units. Standardized coefficients, meanwhile, provide an effective way to compare the relative importance of predictors within a model, helping students prioritize their findings. Yet, they may obscure the actual magnitude of change in the dependent variable. Let’s discuss these advantages and limitations in greater detail to help students use them effectively in assignments.

Benefits of Using Unstandardized Coefficients

Unstandardized coefficients preserve the natural units of the data, providing tangible interpretations. They are invaluable when assignments require predicting actual values or understanding practical implications.

For instance, in public policy assignments, understanding how each additional unit of education translates to increased earnings can inform policy recommendations directly relevant to stakeholders.

Advantages of Standardized Coefficients

Standardized coefficients shine when comparing the relative importance of predictors. Since they eliminate the issue of differing units, they simplify the task of identifying which predictors matter most. This feature is especially useful in assignments with diverse independent variables.

Furthermore, standardized coefficients provide clarity in communication, making results easier to understand for broader audiences or in cross-disciplinary contexts.

When to Use Standardized or Unstandardized Coefficients in Assignments

Choosing when to use standardized or unstandardized coefficients is crucial for successful data interpretation. In assignments, the choice depends on the specific goals of the analysis. If precise predictions in original units are needed, unstandardized coefficients should be used. Conversely, if the goal is to compare the strength of different predictors in explaining the dependent variable, standardized coefficients are the better choice. Understanding when and why to use each type of coefficient ensures that analyses are meaningful, accurate, and aligned with the assignment’s objectives. Let’s break this down to help you decide which to use in different scenarios.

Using Unstandardized Coefficients in Prediction Tasks

For assignments requiring precise predictions, such as forecasting sales revenue or customer engagement, unstandardized coefficients are essential. They retain the units of measurement, allowing students to translate findings directly into actionable insights.

For instance, predicting a company's future revenue based on advertising spend requires unstandardized coefficients to produce dollar-value estimates, which are critical for budgeting and planning.

Employing Standardized Coefficients in Comparative Analysis

When the assignment focuses on assessing the comparative impact of predictors, standardized coefficients are more appropriate. They strip away unit-based noise, enabling fair comparisons and identifying which predictors drive the dependent variable the most.

In assignments exploring social determinants of health, standardized coefficients can reveal whether education, income, or social support has the greatest effect on health outcomes, independent of their original units.

Conclusion

Interpreting standardized and unstandardized coefficients is a vital skill for students working on statistics assignments. Unstandardized coefficients offer clear, real-world interpretations tied to the original units of measurement, making them invaluable for prediction and tangible insights. In contrast, standardized coefficients remove the issue of scale, enabling direct comparisons of predictors' relative influence within a model.

Students should understand when to use each type of coefficient. Assignments requiring precise, real-world predictions typically benefit from unstandardized coefficients. In contrast, those focusing on comparing predictor importance are best served by standardized coefficients.

Moreover, it’s essential to recognize that both types of coefficients have limitations. Unstandardized coefficients do not facilitate comparisons across variables with different units, while standardized coefficients, although useful for comparisons, may obscure the true magnitude of changes in the original units.

By thoughtfully incorporating standardized and unstandardized coefficients, students can produce thorough, insightful analyses that meet the highest academic standards. Applying these concepts not only strengthens their statistical assignments but also builds a solid foundation for future analytical endeavors. Remember, the key to effective analysis lies in understanding the data's context and aligning the interpretation of coefficients accordingly.