How to Analyze Complex Data Relationships on Statistics Assignments Using Partial Correlation

Partial correlation measures the strength and direction of the relationship between two variables while holding one or more other variables constant. Unlike Pearson’s correlation, which only assesses the direct association between two variables, partial correlation accounts for confounding influences.

For example:

• Suppose a study examines the relationship between exercise frequency and weight loss.
• However, diet quality also affects weight loss.
• A simple correlation might suggest a strong link between exercise and weight loss, but this could be partly due to diet.
• Partial correlation controls for diet, revealing the true effect of exercise alone.

Why Is Partial Correlation Important?

Many statistical relationships are influenced by external variables. Without controlling for these factors, researchers risk drawing incorrect conclusions. Partial correlation helps in:

• Identifying true relationships by removing spurious correlations.
• Improving model accuracy in regression analysis.
• Testing hypotheses more rigorously by accounting for confounding variables.

Mathematical Foundation of Partial Correlation

Partial correlation is derived from Pearson’s correlation coefficients but extends the concept to account for additional variables. The calculation involves comparing the correlations between all pairs of variables involved.

Formula for Partial Correlation

The partial correlation between variables X and ;Y, controlling for Z, is calculated as:

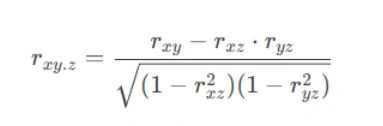
Where:

rxy = Pearson correlation between X and Y

rxz = Pearson correlation between X and Z

ryz = Pearson correlation between Y and Z

The result (rxy.z) ranges from -1 to 1, where:

• 1 = Perfect positive correlation (after controlling for Z)
• -1 = Perfect negative correlation (after controlling for Z)
• 0 = No correlation (after controlling for Z)

Step-by-Step Calculation

1. Compute Pearson Correlations:

Calculate rxy, rxz, and ryz.

2. Plug into the Formula:

Subtract the product of rxz and ryz from rxy.

Divide by the square root of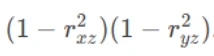

3. Interpret the Result:

A high absolute value indicates a strong relationship after accounting for Z.

Example Calculation

Suppose we have:

rxy= 0.6 (Exercise and Weight Loss)

rxz= 0.5 (Exercise and Diet)

ryz= 0.7(Weight Loss and Diet)

Then:

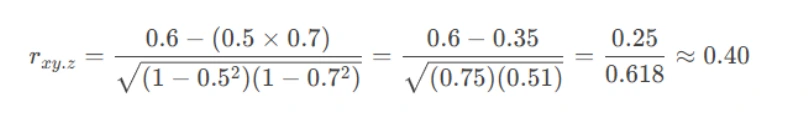
The partial correlation is 0.40, meaning exercise still has a moderate positive effect on weight loss even after controlling for diet.

Applications of Partial Correlation in Research

Partial correlation is widely used in psychology, economics, medicine, and social sciences to uncover true relationships in complex datasets.

Use in Psychology and Behavioral Studies

Researchers often study how one behavior influences another while accounting for external factors.

Example:

• Study: Does stress directly affect sleep quality?
• Confounding Variable: Caffeine intake (since it also affects sleep).
• Solution: Compute partial correlation between stress and sleep while controlling for caffeine.

This helps determine whether stress independently impacts sleep or if caffeine is the primary factor.

Economic and Social Science Research

Economists use partial correlation to analyze relationships while controlling for external influences.

Example:

• Research Question: Is education level linked to income?
• Confounding Variable: Work experience (since more experienced workers tend to earn more).
• Solution: Partial correlation between education and income while controlling for work experience.

This reveals whether education has an independent effect on earnings.

Medical and Public Health Studies

Partial correlation helps isolate the effects of treatments or lifestyle factors on health outcomes.

Example:

• Investigation: Does smoking directly affect lung capacity?
• Confounding Variable: Age (since lung function declines naturally with age).
• Solution: Partial correlation between smoking and lung capacity while controlling for age.

This ensures that the observed effect is due to smoking, not just aging.

Interpreting Partial Correlation Results

Understanding the output of partial correlation is crucial for drawing accurate conclusions.

Strength and Direction of the Relationship

• Close to +1: Strong positive relationship (after controlling for other variables).
• Close to -1: Strong negative relationship (after controlling for other variables).
• Near 0: No meaningful relationship remains after accounting for confounders.

Comparing Partial and Simple Correlation

• If partial correlation ≈ simple correlation, the control variable has little influence.
• If partial correlation is much weaker, the control variable was a major confounder.

Example:

• Simple correlation (Exercise & Weight Loss) = 0.60
• Partial correlation (controlling for Diet) = 0.40
• Interpretation: Diet explains part of the relationship, but exercise still has an independent effect.

Limitations and Key Considerations

While partial correlation is useful, it has certain limitations that researchers must consider.

Assumption of Linearity

Partial correlation assumes that relationships between variables are linear. If the true relationship is nonlinear (e.g., curved or threshold effects), partial correlation may not capture it accurately.

Solution:

• Check scatterplots for nonlinear patterns.
• Consider nonlinear regression models if needed.

Sensitivity to Outliers

Like Pearson’s correlation, partial correlation can be distorted by extreme outliers.

Solution:

• Inspect data for outliers before analysis.
• Use robust correlation methods if outliers are present.

Cannot Establish Causation

Partial correlation helps identify associations, but it does not prove causation. Even after controlling for confounders, hidden variables may still influence results.

Solution:

• Use experimental designs (e.g., randomized trials) for causal claims.
• Apply advanced techniques like structural equation modeling (SEM) for deeper analysis.

Conclusion

Partial correlation is a powerful statistical tool for isolating relationships between variables by controlling for external influences. It is widely used in psychology, economics, medicine, and social sciences to uncover true associations in complex datasets. By understanding its mathematical basis, applications, and limitations, researchers and students can make more accurate and meaningful interpretations of their data.

For those working on statistical assignments involving partial correlation, mastering this technique enhances analytical precision and strengthens research conclusions. Further exploration of related methods—such as multiple regression and mediation analysis—can provide even deeper insights into variable relationships.

If you're analyzing data with multiple interacting factors, partial correlation is an essential tool to ensure your findings are robust and reliable.