Assignment Solution: Statistical Analysis and Hypothesis Testing

Problem Description: First Generation College Students

Question Set 1_A: Research Question: Do more than 25% of all World Campus students identify as first-generation students?

Steps:

Figure 0.1: Randomization test for a proportion

1. Hypotheses:

• Null Hypothesis:0.25H0:P≤0.25
• Alternative Hypothesis:0.25HA:P0.25

2. Randomization Distribution:

• Use StatKey to construct a randomization distribution with at least 5000 resamples.

3. P-Value Calculation:

• According to StatKey, the p-value is 0.935 in a right-tailed test.

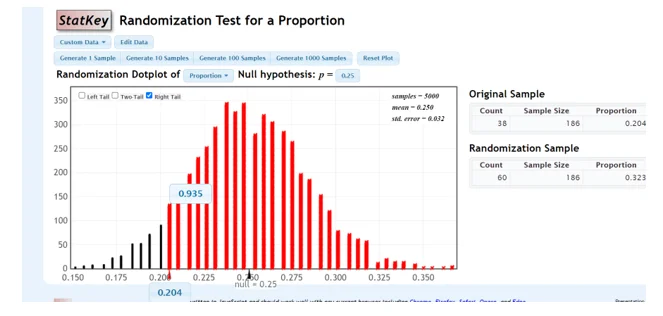
Figure 2: Using StatKey to construct a randomization distribution

4. Decision:

• Since the p-value significance level, fail to reject the null hypothesis.

5. Conclusion:

• We lack sufficient evidence to support the claim that more than 25% of all World Campus students identify as first-generation students.

Question Set 1_C:

• Compare results from parts 1_A and 1_B.
• Explain why the p-value changed with the increase in sample size.
• The p-value changed due to the larger sample size providing more precise estimates of the population proportion, resulting in a narrower distribution around the hypothesized proportion.

Problem Description: Credit Card Fraud Detection

Question Set 2_A: Research Question: Does the new AI technology detect fraudulent charges more than 97% of the time?

Hypotheses:

• Null Hypothesis: 0.97H0:P≤0.97
• • Alternative Hypothesis: 0.97HA:P 0.97

Question Set 2_B: Type I Error:

• Falsely rejects the null hypothesis, indicating the technology detects fraud more than 97% when it does not.
• Consequence: Wasting resources and implementing an ineffective system.

Question Set 2_C: Type II Error:

• Fails to reject the null hypothesis, suggesting the technology does not detect fraud more than 97% when it does.
• Consequence: Missing the chance to enhance fraud detection and exposing customers to fraudulent activity.

Question Set 2_D: Severity Comparison:

• In this scenario, a Type II error is more serious. Failing to invest in the new technology could lead to continued losses from fraudulent charges and potential harm to customers.

Question Set 2_E: Alpha Level Choice:

• Given the consequences, a lower alpha level (e.g., 0.05) is recommended to reduce the likelihood of Type II error.

Reflection:

• Confidence Level:High confidence in answers grounded in provided information and hypothesis testing principles.
• Challenges:Determining the severity of errors in the specific context was the most challenging aspect.