Exploring the Relationship and Causality between Two Variables

This inquiry goes beyond merely identifying a correlation; it seeks to illuminate the underlying patterns and potential causal links that govern the behaviour of the variables in question. The significance of this endeavour lies in its capacity to provide a nuanced understanding of how changes in one variable might influence the other, contributing to the broader landscape of scientific inquiry. Through the creation of a scatter diagram and the application of correlation coefficients, this exploration ventures into both visual and quantitative realms to decipher the nature of the observed relationship. Ultimately, the hypothesis invites a comprehensive investigation into the causative factors that drive the correlation, recognizing that correlation, while indicative, does not inherently establish the directional influences between variables.

Problem Description:

The correlation analysis assignmentaims to investigate the relationship and potential causality between two variables through the use of a scatter diagram and correlation coefficient analysis.

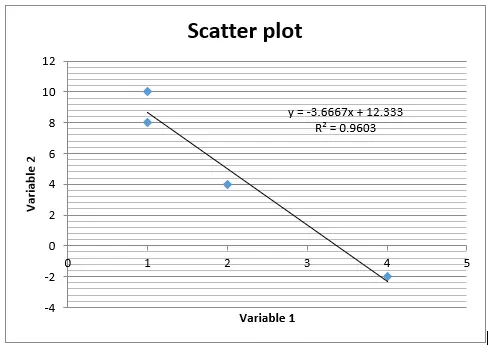
Figure 1: Creating a Scatter Diagram

Description of the General Pattern of Correlation:

The scatter diagram reveals a robust negative linear relationship between Variable 1 and Variable 2. As Variable 1 increases, Variable 2 consistently decreases, forming a tight cluster along a descending straight line.

Correlation Coefficient (r):

The correlation coefficient (r) quantifies this linear relationship, with a calculated value of -0.98. This exceptionally close-to -1 value signifies an extremely strong negative correlation, indicating that as Variable 1 increases, Variable 2 decreases almost perfectly in a linear fashion.

Explaining the Logic:

Correlation, a statistical measure, helps unveil patterns between two variables. In this scenario, Variable 1 and Variable 2 undergo scrutiny. The scatter plot and correlation coefficient reveal the strength and direction of this pattern. With a correlation coefficient of -0.98, the data suggests that changes in Variable 1 are highly predictive of changes in Variable 2. However, correlation alone cannot establish causation.

Possible Directions of Causality:

Determining causality solely from correlation is challenging, but three logically plausible directions are considered:

• Variable 1 causes changes in Variable 2: Implies that alterations in Variable 1 directly influence Variable 2. Improving Variable 1 might lead to a corresponding decrease in Variable 2.
• Variable 2 causes changes in Variable 1: Suggests that changes in Variable 2 drive changes in Variable 1. This direction, while possible, may be less intuitive based on the nature of the variables.
• Third Variable: A third unconsidered variable might be influencing both Variable 1 and Variable 2, creating a false appearance of a direct relationship.

Correlational vs. Cause-and-Effect Studies:

Correlational studies explore relationships without manipulating variables, utilizing correlation coefficients for quantification. However, they do not imply causation. Cause-and-effect studies, often experimental, manipulate variables to demonstrate direct causality. The key distinction lies in the ability to infer causation: correlational studies identify relationships, while cause-and-effect studies seek to prove causality through manipulation and control of variables.