SAH icon
A New Look is Coming Soon
StatisticsAssignmentHelp.com is improving its website with a more improved User Interface and Functions
 +1 (315) 557-6473 

Unraveling Crime Dynamics: A Regression Analysis of Population, Police Presence, and Crime Rates Using Stata

In this assignment, we embark on a journey through sophisticated regression analysis, utilizing the powerful statistical tool, Stata. This study delves into the intricate relationships between crime rates, population size, and the presence of police officers. Through meticulous examination, we unearth compelling insights. The results showcase the interplay between these factors and demonstrate the essential role of controlling for population size. This analysis provides a deeper understanding of the dynamics shaping crime rates, shedding light on the multifaceted nature of law enforcement and societal influences.

GET FREE QUOTE
  1. Home
  2. Crime Rate Regression Analysis: Insights with Stata

Problem Description

In this assignment, we perform regression testing on the relationship between crime rates, population size, and the number of police officers using the statistical software Stata. The objective is to analyze how population size and the presence of police officers influence crime rates. We aim to understand the correlation between these variables and the impact of controlling for population size in our analysis.

Answer 1: a) Expectations and Assumptions:

i) We anticipate that the coefficient (β2) relating population size to the number of crimes will be positively correlated, suggesting that as the population size increases, there is a likelihood of higher crime rates.

ii) In the regression of officers on population, we expect to observe a positive coefficient, indicating a positive correlation between the number of police officers and the population.

1: Regression analysis of officers on the population

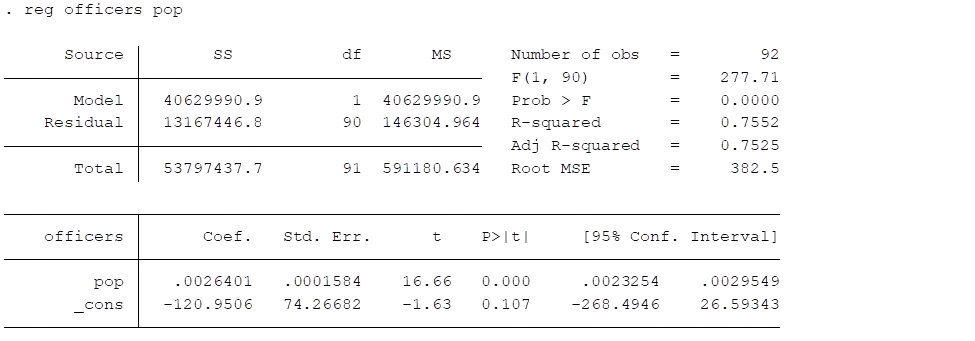
Table 1: Regression analysis of officers on the population

iii) Anticipating that crimes may grow more rapidly with an increase in population compared to police officers, we expect an upward bias in the regression for crimes on officers once we remove the population control variable.

b) Regression without Population as a Control Variable: The regression equation is as follows:

Crimes = 8831.457 + 33.3999 * Officers

The coefficient of officers (33.3999) in this model suggests that, on average, an increase of one police officer in a city results in 33 more crimes, and vice versa.

c) Regression with Population as a Control Variable: We executed a regression in Stata for crimes on officers and population, and the results are presented below.

In this regression with population as a control variable:

  • The coefficient of "officers" decreased to 14.415, compared to 33.3999 in the regression without population as a control variable.
  • The standard error increased to 3.448, compared to 2.043 in the regression without population as a control variable.

The substantial reduction in the coefficient for officers (almost 50% drop) implies that a portion of the increase in crime rates can be attributed to the size of the population. Controlling for population size results in relatively fewer crimes for a given number of officers, aligning with our expectations.

d) Regression of Residuals: We also performed a regression of the residuals of crime rates on the residuals of the population. The results are as follows:

  • The coefficient of resid_x (14.415) in this regression matches the coefficient of "officers" at 14.415 in the regression for crimes on officers with population as a control variable.
  • Both coefficients are statistically significant, but the standard error for the coefficient of resid_x is slightly larger (3.448) in comparison to the standard error in the regression for crimes on officers with population as a control variable.

Conclusion: Our analysis using regression testing in Stata has revealed the intricate relationship between crime rates, population size, and the number of police officers. Controlling for population size demonstrates a significant reduction in the influence of police officers on crime rates, highlighting the importance of considering population as a key factor in such analyses.